Select menu item <Analysis><Convolution> to apply
the convolution for digitally filtering data.
Convolution
In linear systems convolution is used to describe the relationship
between three signals of interest:
- the input signal Y[i],
- the impulse response F[i] (filter kernel),
- the output signal W[i]
.
Convolution is defined by the convolution sum:
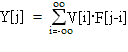
FindGraph includes several filter kernels F(u):
- Common filter kernels (Delta function, Amplification, Attenuation, Inverting, Shift, Echo, First derivative, Integral).
- Low-pass filter kernels to provide an averaging (smoothing) of the signal
(exponential, rectangular, Gauss function, sinc function with Hamming or with Blackman windows).
- High-pass filter kernels.
You can draw your own signal or to modify a selected signal.
Simple click on left chart and use the mouse to draw your own signal.
You can use series of points or any function (formula), you created, as filter F[u]
Correlation
Correlation is a mathematical operation that is very similar to convolution.
Convolution is the relationship between:
- the input signal Y[i],
- the impulse response F[i],
- the output signal W[i]
.
This output signal is called the cross-correlation of the two input signals:
 Read more: The Scientist and Engineer's Guide to Digital Signal Processing
by Steven W. Smith, Ph.D.
Read more: The Scientist and Engineer's Guide to Digital Signal Processing
by Steven W. Smith, Ph.D.

á
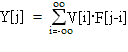
 Read more: The Scientist and Engineer's Guide to Digital Signal Processing
by Steven W. Smith, Ph.D.
Read more: The Scientist and Engineer's Guide to Digital Signal Processing
by Steven W. Smith, Ph.D.